Deep Learning based Relative Localization
underwater relative localization using 6D pose estimation
Publications
- B. Joshi, Md Modasshir, T. Manderson, H. Damron, M. Xanthidis, A. Q. Li, I. Rekleitis, and G. Dudek, “DeepURL: Deep Pose Estimation Framework for Underwater Relative Localization,” In IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2020
- M. Xanthidis, B. Joshi, M. Roznere, W. Wang, N. Burgdorfer, A. Q. Li, P. Mordohai, S. Nelakuditi, and I. Rekleitis, “Towards Mapping of Underwater Structures by a Team of Autonomous Underwater Vehicles”, In Robotics Research, 2023
In a GPS-denied environment, it is desirable for a team of robots to localize with respect to each other. For cooperative mapping, the robots need to localize in a common global reference frame. A deep learning based 6D pose estimation framework for underwater relative localization; so that AUVs can be represented in common reference frame. Due to the profound difficulty of collecting ground truth images with accurate 6D poses underwater, we utilize rendered images from the Unreal Game Engine for training. CycleGAN, an image-to-image translation network, is employed to bridge the gap between the rendered and the real images producing synthetic images for training. The two-stage pipeline first predicts 2D image keypoints representing eight corners of the 3D model of the AUV, and then the 6D pose in the camera coordinates is determined using RANSAC-based PnP. The deep learning framework has been tested in different environments – pool, ocean – and different platforms, including an Aqua2 robot and GoPro cameras, demonstrating its robustness.
Dataset Generation
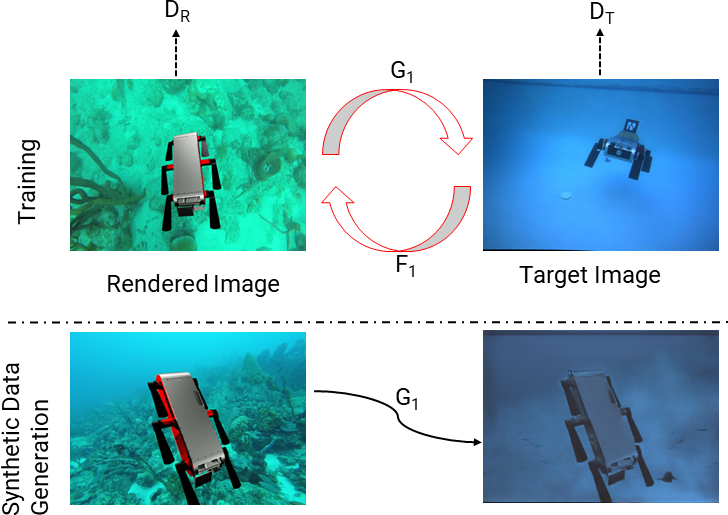
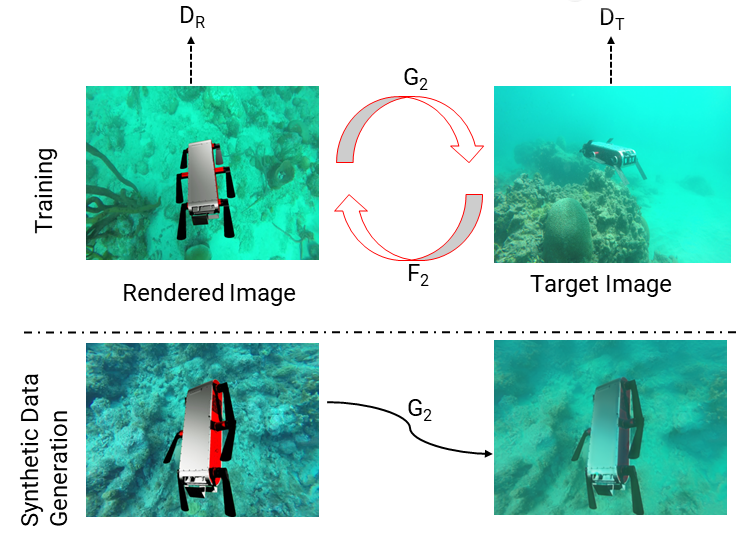
Obtaining training datasets with corresponding accurate 6D pose ground truth is not trivial underwater. We mitigate the requirement for annotated 6D pose using domain adaptation. We utilize Unreal Engine 4 (UE4) with a 3D model of the Aqua2 robot swimming, projected over underwater images to generate training images with known poses. These rendered images differ from actual underwater images that suffer from color loss and poor visual quality. This hampers the performance of classical deep learning-based 6D pose estimation methods in the underwater domain. CycleGAN was employed to transform UE4 rendered images to image sets used for training with varying appearances, similar to real-world underwater images. We use two target domains: one resembling the pool environment and the other resembling the ocean environment.
Pose Estimation Framework
In the training process, UE4 renders a 3D model of Aqua2 with known 6D poses projected on top of underwater ocean images. The feature space between real underwater and rendered images is aligned by transferring the rendered images to target domains (swimming pool and ocean) using CycleGAN. The next stage consists of a Convolutional Neural Network (CNN) that predicts the 2D projections of the 8 corners of the object’s (Aqua2) 3D model, and an object detection bounding box. In our approach, each grid cell inside the bounding box predicts the 2D projections of keypoints along with their confidence focusing on local regions belonging to the object. These predictions of all cells are then combined based on their corresponding confidence scores using RANSAC-based PnP during 6D pose estimation.
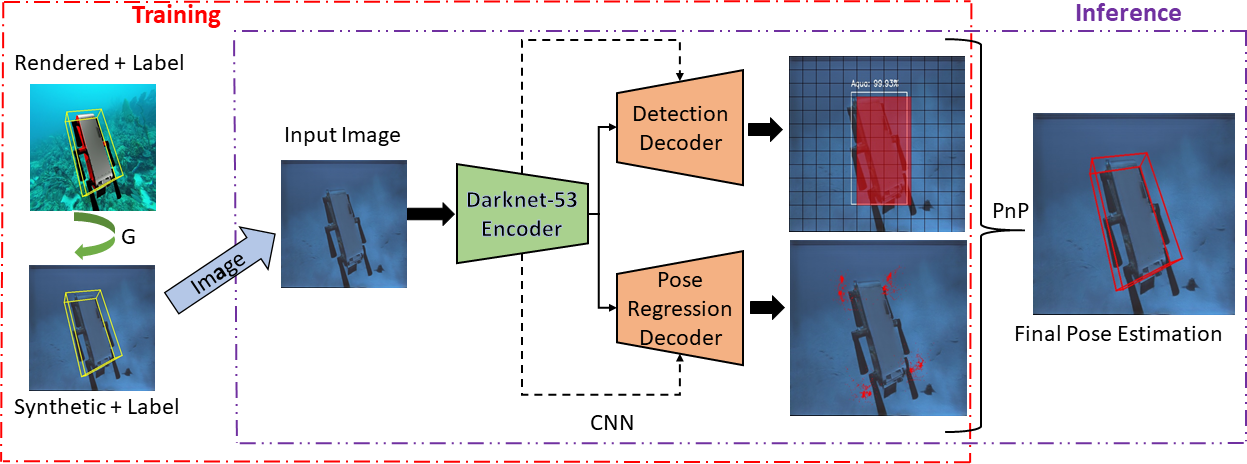
The network consists of an encoder, Darknet-53, and two decoders: Detection Decoder and Pose Regression Decoder. The detection decoder detects objects with bounding boxes, and the pose regression decoder regresses to 2D corner keypoints of the 3D object model. The decoders predict the output as a 3D tensor with a spatial resolution of \(S × S\) and a dimension of \(D_{det}\) and \(D_{reg}\) , respectively. The spatial resolution controls the size of an image patch that can effectively vote for object detection and the 2D keypoint locations. The feature vectors are predicted at three different spatial resolutions. Predicting in multiple spatial resolutions with upsampling helps to obtain semantic information at multiple scales using fine-grained features from early on in the network. The object detection stream is similar to YOLOv3.
Pose Regression Stream
The pose regression stream predicts the location of the 2D projections of the 8 corners associated with the 3D object model of Aqua2. The pose regression stream predicts a 3D tensor with size \(S × S × D_{reg}\) . We predict the (x, y) spatial locations for the 8 keypoint projections along with their confidence values, \(D_{reg} = 3 × 8\). We predict the offset of each keypoint from the corresponding grid cell in the following way: Let c be the position of the grid cell from the top left image corner. For the \(i^{th}\) keypoint, we predict the offset \(f_i(c)\) from the grid cell so that the actual location in image coordinates becomes \(c + f_i(c)\), which should be close to the ground truth 2D locations \(g_i\). The residual is calculated as
\[\Delta_i(c) = c + f_i(c) - g_i\]and we define offset loss function, \(L_{off}\), for spatial residual:
\[L_{\textrm{off}} = \sum_{c \epsilon B} \sum_{i=1}^{8} \left \lvert \lvert \Delta_i(c) \right \rvert \rvert_1\]where B consists of grid cells that fall inside the object bounding box and \(||.||_1\) represents L1-norm loss function, which is less susceptible to outliers than L2 loss. Only using grid cells falling inside the object bounding box for 2D keypoint predictions focuses on image regions that truly belong to the object. Apart from the 2D keypoint locations, the pose regression stream also calculates the confidence value \(v_i(c)\) for each predicted point. The confidence value should be representative of the distance between the predicted keypoint and ground truth values. A sharp exponential function of the 2D euclidean distance between prediction and ground truth is used as confidence. The confidence loss is calculated as
\[L_{\textrm{conf}} = \sum_{c \epsilon B} \sum_{i=1}^{8} \left \lvert \lvert v_i(c) - exp(-\alpha \left \lvert \lvert \Delta_i(c) \right \rvert \rvert_2) \right \rvert \rvert_1\]where \(\left \lvert \lvert . \right \rvert \rvert_2\) denotes euclidean distance or L2 loss and parameter α defines the sharpness of the exponential function. The pose regression loss takes up the form
\[L_{\textrm{reg}} = \lambda_{\textrm{off}}L_{\textrm{off}} + \lambda_{\textrm{conf}}L_{\textrm{conf}}\]Pose Refinement
During inference, our network’s object detection stream predicts the bounding boxes’ coordinate locations with their confidences and the class probabilities for each grid cell. Simultaneously, the pose regression stream produces the projected 2D locations of the object’s 3D bounding box and their confidence scores for each grid cell. The 2D keypoint predictions for grid cells that fall outside of the bounding box from the object detection stream are filtered out. The keypoints with confidence scores less than 0.5 are also filtered out. To balance the trade-off between computation time and accuracy, we empirically found that using the 12 most confident 2D predictions for each 3D keypoint. Hence, we employ RANSAC-based PnP on \(12 × 8 = 96\) 2D-to-3D correspondence pairs between the image keypoints and the object’s 3D model to obtain a robust pose estimate.

Results
We evaluated the performance of the pose estimation network on three datasets captured using the Aqua2 robot and GoPro camera in a pool and an open sea environment. The pool dataset contains groundtruth and is used for quantitative evaluation. The GoPro dataset is only used for qualitative evaluation. To evaluate the pose accuracy, we use standard metrics - namely- 2D reprojection error and the average 3D distance of the model vertices, referred to as ADD metric. We also calculate the translation and orientation error. In the case of reprojection error, we consider the pose estimate to be correct if the average distance between 2D projections of 3D model points obtained using predicted and groundtruth poses is below a 10 pixels threshold, referred to as REP-10px. The ADD metric takes poseestimate as correct if the mean distance between the coordinates of the 3D model vertices transformed by estimated and ground truth pose falls below 10% of the model diameter, referred to as ADD-0.1d.
Pool Dataset
To generate our pool dataset, we deployed two robots: one robot observing the other with a vision-based 2D fiducial marker (AR-tag mounted on the top used to estimate ground truth during two pool trials in indoor and outdoor pools). Approximately 11K images were collected with estimated localization, provided from the pose detection of the AR tag and the relative transformation of the mounted tag to the real robot. The dataset contains images with a distance between two Aquas ranging between 0.5m to 3.5m.
| Method | Translation error (cm) | Orientation error (deg) | REP-10px Accuracy | ADD-0.1d Accuracy | FPS |
|---|---|---|---|---|---|
| Tekin et al. | 27.8 | 18.87 | 9.33% | 23.39% | 54 |
| PVNet | 48.6 | 24.55 | 23.22% | 43.09% | 37 |
| DeepURL | 6.8 | 6.77 | 25.22% | 57.16% | 40 |
Translation and rotation errors along with REP-10px and ADD-0.1d accuracy for the pool dataset are presented in Table above, as well as the runtime comparisons on Nvidia RTX 2080.
Barbados GoPro Dataset
We collected images underwater in Barbados of an Aqua2 robot swimming over coral reefs using a GoPro camera, which differ significantly from the images collected using another Aqua2 in terms of hue, image size, and aspect ratio.
Citation
If you find this work useful in your research, please consider citing:
@inproceedings{deepurl,
author = {Bharat Joshi and Md Modasshir and Travis Manderson and Hunter Damron and Marios Xanthidis and Alberto {Quattrini Li} and Ioannis Rekleitis and Gregory Dudek},
title = {DeepURL: Deep Pose Estimation Framework for Underwater Relative Localization},
booktitle = {IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS)},
year = {2020},
pages={1777-1784},
doi={10.1109/IROS45743.2020.9341201},
}