Real-Time Dense Mapping
real-time underwater dense reconstruction
Publications
- W. Wang, B. Joshi, N. Burgdorfer, K. Batsos, A. Quattrini Li, P. Mordohai, and I. Rekleitis, “Real-Time Dense 3D Mapping of Underwater Environments,” IEEE International Conference on Robotics and Automation (ICRA), 2023
We present a real-time, scalable, detailed underwater dense reconstruction pipeline utilizing SVIn2, a robust VIO method. The pipeline architecture incurs an almost constant computational load by processing fixed-length segments of the data at a time. The proposed approach includes: robust real-time camera pose estimation using SVIn2 which fuses information from the cameras and IMU; two-stage depth map estimation based on multi-threaded CPU-based stereo matching followed by visibility-based depth map fusion; and colored point cloud generation. We conducted a thorough evaluation comparing our method to COLMAP, which is the state-of-the-art open-source 3D reconstruction framework. Our evaluation considers run-time, depth map estimation, and dense reconstruction on four challenging underwater datasets.
Overview
Our approach to 3D reconstruction relies on two parallel components: (1) a multi-sensor SLAM system, SVIn2, and (2) a real-time dense 3D mapping system; see figure below.
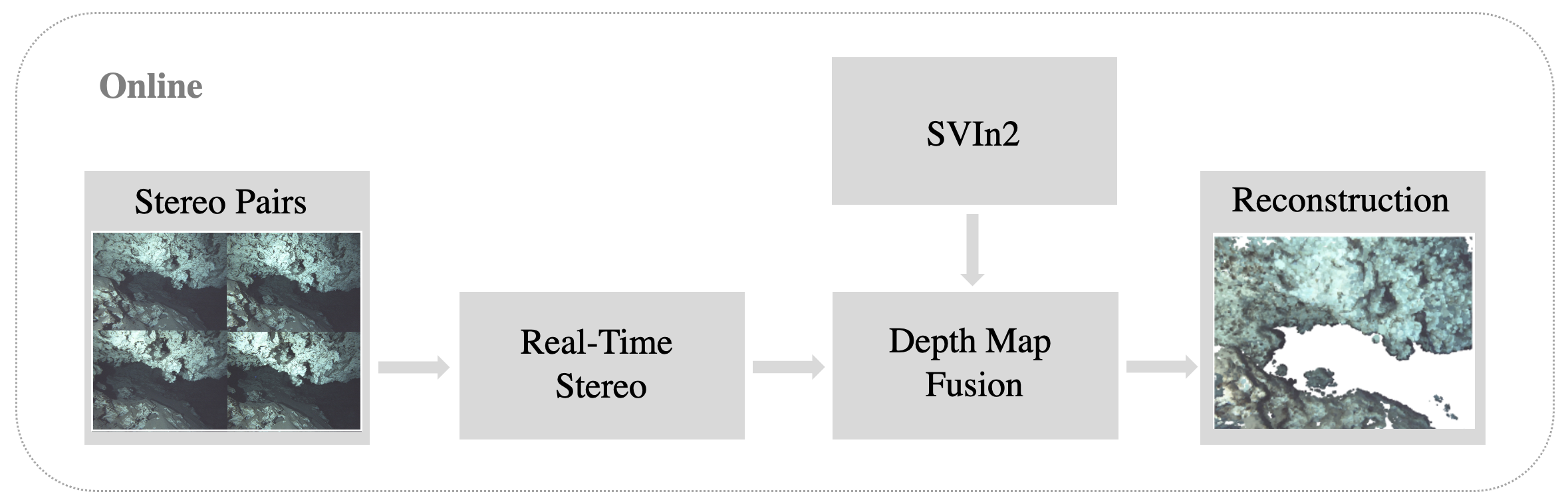
Robot pose estimation relies on our previous work, SVIn2, a tightly-coupled keyframe-based SLAM system that fuses data from the cameras and IMU.
Depth Map Estimation
The stereo matching module estimates depth for every pixel of the left image of a stereo pair of images. We are able to process stereo pairs at high throughput leveraging multi-threaded CPU implementations (OpenMP) without relying on GPUs. The implementation of matching cost computation is publicly available ( Code ).
Matching Cost Computation
Stereo matching estimates the likelihood for each possible disparity that can be assigned to a given pixel of the reference image. Disparity \(d\) is defined as the difference between the horizontal coordinates of two potentially corresponding pixels in the same epipolar line (scanline) in the left and right image. Disparity is inversely proportional to depth \(Z\), which can be computed as:
\[Z = \frac{bf}{d}\]where \(b\) is the baseline (distance) between the camera centers and \(f\) is the focal length.
To select the most likely disparity for each pixel in the left image, we assess the photoconsistency of that pixel with potentially matching pixels in the conjugate epipolar line in the right image. This is accomplished by computing a similarity or dissimilarity measure in matching windows centered around the pixels under consideration. We used the Sum of Absolute Differences (SAD), which is a dissimilarity (cost). The cost values for all pixels and disparities are accumulated in the cost volume \(V\), which is computed as follows with SAD:
\[V(x_L,y,d) = \sum_{(u,v)\in W(x_L,y)} |I_L(u,v)-I_R(u-d,v)|\]where \(I_L\) and \(I_R\) are the two images and \(W(x_L,y)\) is the matching window.
Optimization
The fastest way to obtain a disparity map from the cost volume is by selecting the disparity with the smallest cost for each pixel. To obtain higher accuracy the cost volume can be optimized by the widely-used Semi-Global Matching algorithm (SGM). SGM is used for extracting a disparity map that approximately optimizes a global cost function defined over 2D image neighborhood by combining multiple 1D cost minimization problems. Disparity is converted to depth, which is then refined to sub-pixel precision by fitting a parabola in the vicinity of the minimum optimized cost.
Confidence Estimation
Depth map fusion benefits from confidence values conveying which depths are more reliable. We attach a confidence to each depth after SGM using the PKRN measure, which is the ratio of the second smallest over the smallest cost for that pixel in the cost volume.
Depth Map Fusion
Depth maps estimated by the stereo matching module are reasonably accurate but contain noise due to lack of texture, occlusion, and motion blur. Depth map fusion takes as input overlapping depth and detects consensus among depth estimates and violations of visibility constraints as evidence for which depths are correct and which are likely to be outliers.
We denote depths rendered on the reference view by \(Z_j\) and depths in their original camera coordinate systems by \(Z^o_j\). For each of the depth candidates \(Z_j\) we accumulate support and visibility violations. Support comes from other depth candidates for the same pixel that are within a small distance of \(Z_j\). \(Z_j\) is then replaced by the weighted average of the supporting depths, with confidence values serving as weights. The confidence of the blended depth estimate \(Z^s_j\) is set equal to the sum of the supporting confidences.
\[Z^s_j = \frac{s_{ij}Z_i}{s_{ij}}, \ \ \ s_{ij}=T(||Z_i-Z_j||<\epsilon)\] \[C^s_j = \frac{s_{ij}C_i}{s_{ij}}, \ \ \ s_{ij}=T(||Z_i-Z_j||<\epsilon)\]where \(s_{ij}\) is a boolean variable indicating whether \(Z_i\) and \(Z_j\) support each other and \(T()\) is the indicator function which is 1 when its argument is true.
There are two types of violations of visibility constraints: occlusions and free space violations. An occlusion occurs when \(Z_j\) appears behind a rendered depth map from view \(k\), \(Z_k\), on the ray of the reference view, while a free space violation occurs when \(Z_j\) appears in front of an input depth map \(Z^o_l\) on the ray of view \(l\).
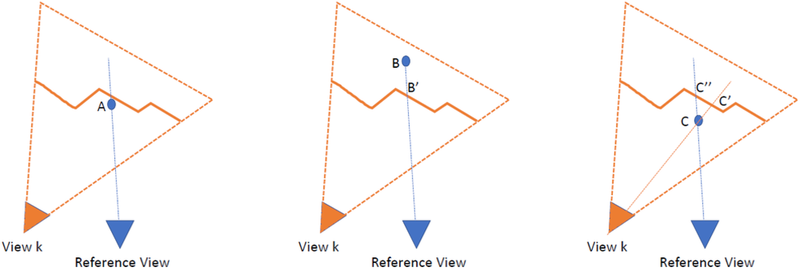
Detected violations do not result in updates to the fused depth, but the corresponding confidence is reduced by the confidence of the conflicting estimate. We assign to each pixel the depth with the highest fused confidence, after adding support and subtracting conflicts. We then threshold confidence to reject outliers.The fusion process is independent across pixels, and is thus parallelizable. Rendering depth candidates to the original depth maps to detect free space violations is the most expensive step. Fusion operates in pipeline mode keeping a small number of recent depth maps in memory at a given time. At the next time step, the oldest depth map in the sliding window is dropped and it is replaced by the most recent one.
Experimental Results
We evaluate both the sparse and dense components of the 3D reconstruction system and compare them to the corresponding aspects of COLMAP, which operates much slower in offline mode.
Datasets
The datasets are collected using a custom made sensor suite and an Aqua2 robot. Both devices are equipped with two iDS USB3 uEye cameras as stereo pair and a MicroStrain 3DM-GX4-15 IMU. The stereo images are recorded at 15 Hz; inertial data at 100 Hz. We use the following datasets see figure below:
- Ginnie Ballroom, Gennie Springs, FL, USA
- Cenote, QR, Mexico
- Coral Reef, Barbados
- Stavronikita Shipwreck, Barbados




These datasets form a diverse set of underwater environments, including open, flat areas of the seafloor, dense and richly structured shipwrecks, and enclosed caverns with relatively uniform surfaces.
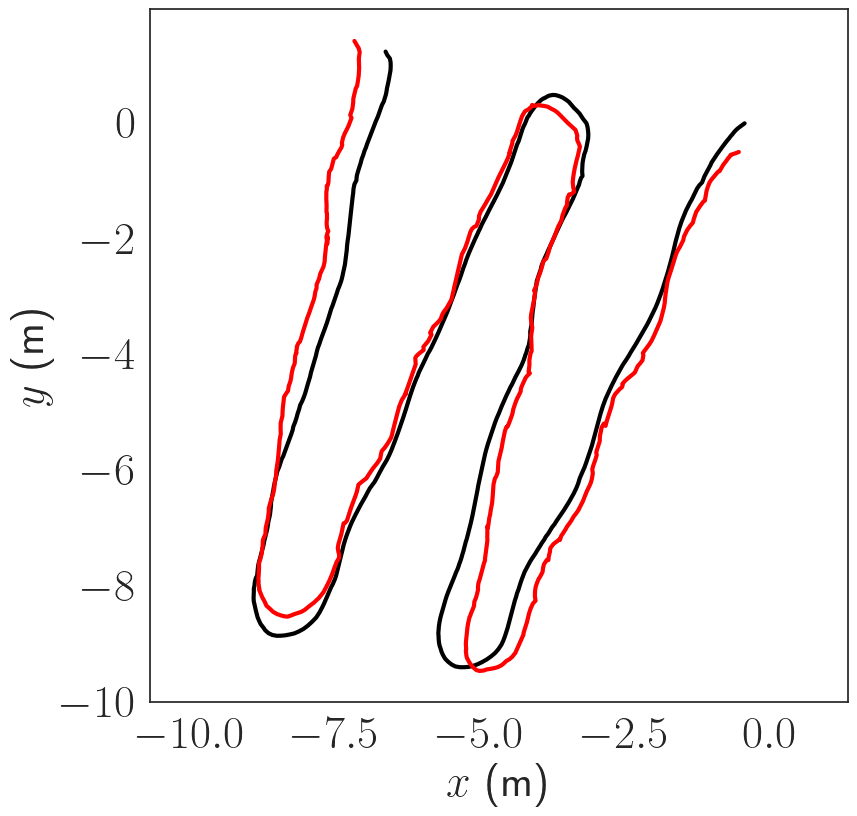
Pose Estimation Results
The trajectories are estimated using COLMAP scaled using the known stereo baseline. The trajectories are then compared in terms of absolute trajectory error (ATE) after sim(3) alignment. The trajectories are in general consistent up to a few cm in terms of ATE.
| Dataset | length[m] | RMSE [m] |
|---|---|---|
| Ginnie Ballroom | 98.73 | 0.07 |
| Cenote | 67.24 | 0.019 |
| Coral Reef | 45.52 | 0.39 |
| Stavronikita | 106.30 | N/A |
We were unable to obtain continuous trajectory for the Stavronikita dataset due to segments in which the AUV maneuvered over the side of the wreck, thus facing open water. Thus, we use the COLMAP trajectory for the Stavronikita dataset.
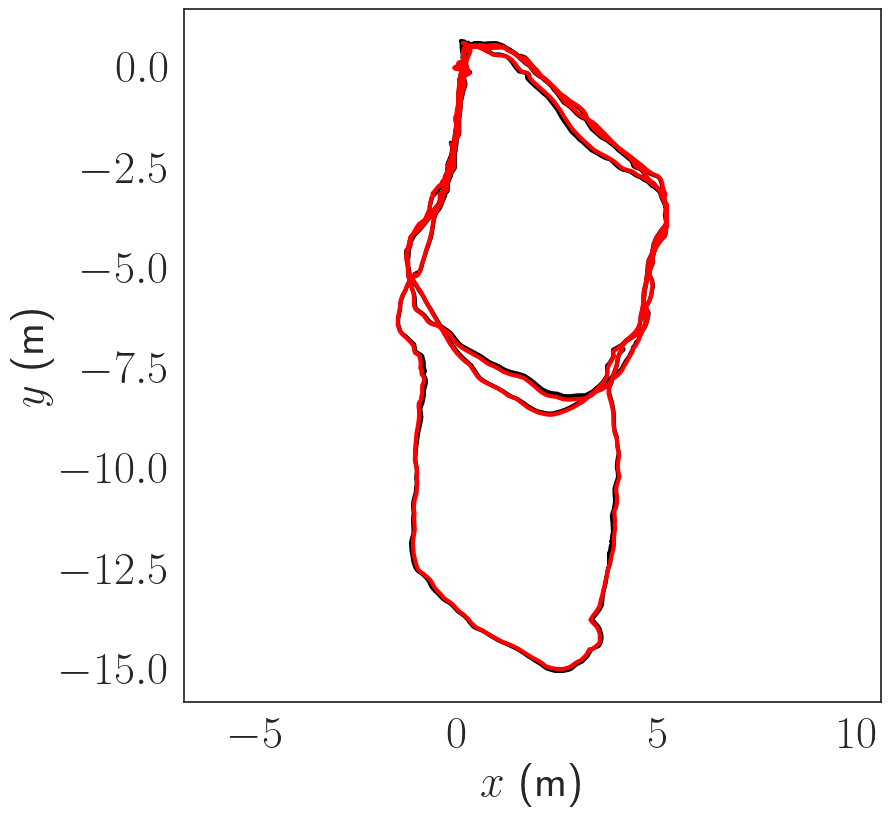
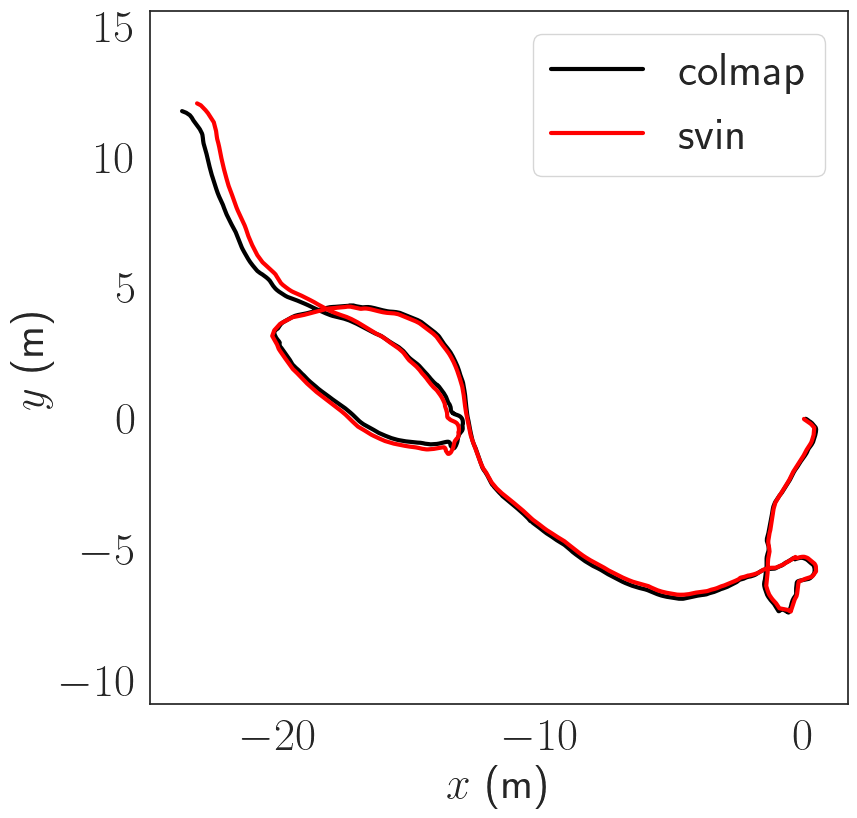
Dense Reconstruction Results
We compare the depth maps and 3D point cloud generated by our pipeline with COLMAP. In the four datasets (Ginnie Ballroom, Cenote, Coral Reef, Stavronikita) that we consider, there are 13671, 3519, 3207, 8824 stereo pairs and 1519, 1401, 631 and 897 keyframes selected by SVIn2, respectively. The comparison of run-times on the keyframes between COLMAP and our pipeline is shown in table below
| Dataset | Stereo Pairs | COLMAP Runtime (min) | Pipeline Runtime (min) |
|---|---|---|---|
| Ginnie Ballroom | 1519 | 858.10 | 22.36 |
| Cenote | 1401 | 1250.53 | 20.92 |
| Coral Reef | 631 | 337.99 | 12.44 |
| Stavronikita | 897 | 482.57 | 14.95 |
Both COLMAP and the pipeline produce dense depth maps, which, however, contain some holes without depth estimates due to filtering.
Next, we compare the reconstruction from COLMAP and our pipeline based on recall and precision. To account for discrepancy in dense reconstruction resulting from camera pose tracking error, we use the RMSE error between SVIn2 and COLMAP poses as a threshold to compute precision and recall.
| Dataset | threshold (m) | pipeline-to-colmap Precision (%) | colmap-to-pipeline Recall (%) |
|---|---|---|---|
| Ginnie Ballroom | 0.07 | 85.6 | 92.0 |
| Cenote | 0.19 | 91.2 | 89.0 |
| Coral Reef | 0.39 | 81.8 | 85.9 |
The results show that the dense reconstructions obtained using SVIn2 poses are accurate compared to those of COLMAP, with both precision and recall over 80% for all datasets.
Citation
If you find this work useful, please consider citing our paper:
@inproceedings{underwater_dense_reconstruction,
author = {Weihan Wang and Bharat Joshi and Nathaniel Burgdorfer and Konstantinos Batsos and
Alberto {Quattrini Li} and Philippos Mordohai and Ioannis Rekleitis},
title = {Real-Time Dense 3D Mapping of Underwater Environments},
booktitle = {IEEE International Conference on Robotics and Automation (ICRA)},
year = {2023},
}